

Thus, the area of the scalene triangle, with a base 'b and height 'h' is expressed as Area of scalene triangle = 1/2 × b × h What is the Formula Used for Finding the Area of a Right Triangle? The area of a scalene triangle is half of the product of the base and the height of the triangle. No, an isosceles triangle can be an acute angle, right angle, or obtuse-angled triangle depending upon the measure of the angles it has. There are six types of triangles categorized on the basis of sides and angles as listed below: How many Types of Triangles are there in Maths? Perimeter of a triangle, P = (a + b + c) where 'a', 'b', and 'c' are the 3 sides of the triangle.Area of triangle, A = where 'b' is the base of the triangle and 'h' is the height of the triangle.These triangle formulas can be mathematically expressed as The two basic triangle formulas are the area of a triangle and the perimeter of a triangle. What are the Two Basic Triangle Formulas? It is a simple polygon in which the 3 vertices are joined with each other and it is denoted by the symbol △. In geometry, a triangle is defined as a two-dimensional shape with three sides, three interior angles, and three vertices. Area and Perimeter of Triangle WorksheetsįAQs on Triangle What is a Triangle in Maths?.The sum of the interior angles of a triangle is 180° and is expressed as ∠1 + ∠2 + ∠3 = 180°.Ĭheck out these interesting articles to know more about triangles and topics related to triangles.There are two important formulas related to triangles, i.e., the Heron's formula and Pythagoras theorem.The following figure shows the different kinds of triangles categorized on the basis of sides and angles. Let us understand the classification of triangles with the help of the table given below which shows the difference between 6 different types of triangles on the basis of angles and sides. You also should now see the connection between the Isosceles Triangle Theorem to the Side Side Side Postulate and the Angle Angle Side Theorem.Triangles can be classified on the basis of their sides and angles. The converse of the isosceles triangle theorem is true! Lesson summaryīy working through these exercises, you now are able to recognize and draw an isosceles triangle, mathematically prove congruent isosceles triangles using the isosceles triangles theorem, and mathematically prove the converse of the Isosceles Triangles Theorem. With the triangles themselves proved congruent, their corresponding parts are congruent (CPCTC), which makes BE ≅ BR. The Angle-Angle-Side Theorem states that If two angles and the non-included side of one triangle are congruent to the corresponding parts of another triangle, then the triangles are congruent. That would be the Angle-Angle-Side Theorem (AAS). Let's see…that's an angle, another angle, and a side. Since line segment BA is used in both smaller right triangles, it is congruent to itself. Since line segment BA is an angle bisector, this makes ∠EBA ≅ ∠RBA. Now we have two small, right triangles where once we had one big, isosceles triangle: △BEA and △BAR. Where the angle bisector intersects base ER, label it Point A.

Given that ∠BER ≅ ∠BRE, we must prove that BE ≅ BR.Īdd the angle bisector from ∠EBR down to base ER.
To prove the converse, let's construct another isosceles triangle, △BER. Unless the bears bring honeypots to share with you, the converse is unlikely ever to happen. If I attract bears, then I will have honey. If I have honey, then I will attract bears. If I lie down and remain still, then I will see a bear.įor that converse statement to be true, sleeping in your bed would become a bizarre experience.
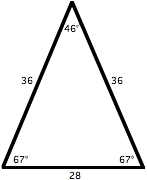
If I see a bear, then I will lie down and remain still. If the premise is true, then the converse could be true or false: If the original conditional statement is false, then the converse will also be false. Now it makes sense, but is it true? Not every converse statement of a conditional statement is true. Converse Of the Isosceles Triangle Theorem


 0 kommentar(er)
0 kommentar(er)
